KPRN : Explainable Reasoning over Knowledge Graphs for Recommendation

2023-06-18

KPRN

논문 : https://ojs.aaai.org/index.php/AAAI/article/view/4470

Introduction

• KG를 사용하지 않는 방식
  • KG를 사용하는 방식 이전에도 유저 프로필, 아이템 속성같은 보조적인 데이터를 추천에 이용하는 방식이 있었음.

• KG를 사용하는 방식

  • KG를 사용하는 방식에서는
    • (Ed Sheeran, IsSingerOf, Shape of You)와 같은 triplets을 사용하여 user-item interaction을 표현한다.
    • users와 items 간 interlinks에는 connectivity(연결성)이 있고, 연결성은 user-item 간 관계를 내포하는데, 이 정보가 추천에 보조적인 정보로 이용된다.
    • connectivity로 인해 KG 추천시스템이 추론(reasoning)과 설명이 가능(explainability) 해짐.

      • 예시

        

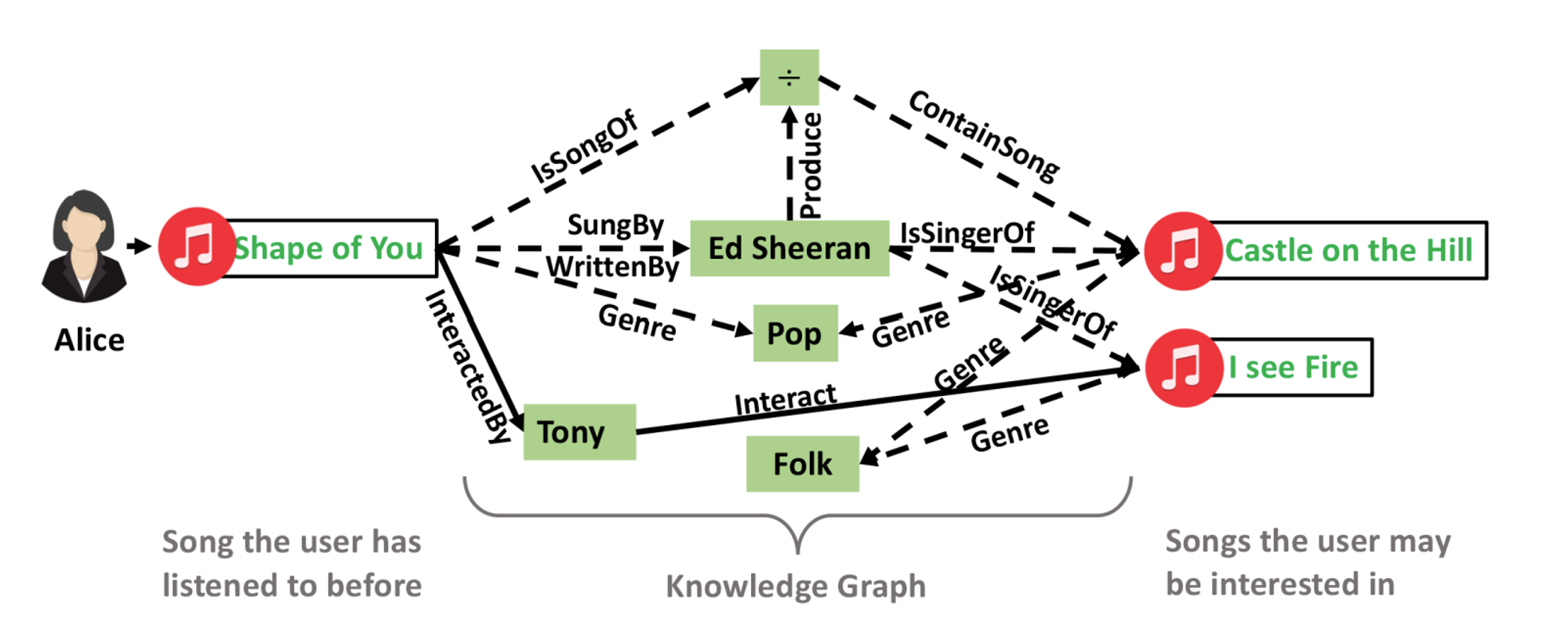
        • Alice는 Shape of You와 연결돼있고, 이는 Ed Sheeren이 부른 노래이다. 이로 인해 Ed Sheeren이 부른 I see Fire에도 Alice는 연결된다.
        • 이러한 연결성이 발생하지 않은 user-item interaction에 대해서 추론을 할 수 있게 해준다. 결과적으로 I see Fire를 Alice하게 추천하게 된다.

        ⇒ connectivity를 modeling하는 방법이 중요하다.

• KG를 사용하는 기존 연구(Related Works)

  • 기존 연구는 Embedding-based Methods와 Path-based Methods라는 두 가지 카테고리로 나눌 수 있다. 본 논문에서는 기존 방법론들은 reasoning이 부족하다는 한계를 주장한다.
  • Embedding-based Methods
    • TransE, TransR 같은 KGE(Knowledge Graph Embedding) 방식
    • KGE는 개체간의 직접적인 관계만 고려하며, 다중 호프(multi-hop) 관계 경로는 고려하지 않는다. 또한, 모든 connectivity를 탐구하지 않고, user-item 연결성을 사용자의 선호도를 추론하는 데까지 이어지지 않아 reasoning이 부족하다.
  • Path-based Methods
    • 관계(relation)들이 메타 경로에서 제외되는 경우, 메타 경로만으로는 경로의 전체적인 의미를 명확하게 특정하기 어렵습니다. 특히 비슷한 개체들이지만 다른 관계가 포함된 경우에는 더욱 어려워진다.
    • 메타 경로는 사전에 도메인 지식을 미리 정의해야 하기 때문에, 보이지 않는 연결 패턴을 자동으로 발견하고 추론하는 데 실패할 수 있다. 따라서 새로운 연결성 패턴에 대해 자동적으로 학습하거나 추론하는 능력이 제한된다.

• 본 논문에서 제안하는 방식

  • entity들의 sequential dependencies와 path 상에 있는 relation들을 모델링하여 reasoning을 잘 하고자 한다.
  • 각각의 경로가 추론할 때 어떤 기여를 하는지를 구별할 수 있는 능력을 가져 설명 가능한 모델을 만든다. 이를 위해 사용자의 관심사를 추론할 때 다른 경로의 다른 기여를 구별할 수 있게 한다.
  • qualified paths를 추출한다.
  • LSTM 모델로 entities와 relations을 모델링한다.

  • pooling operation(attention과 같은 역할)으로 경로 별 다른 기여를 구별할 수 있게 함.

    ⇒ 결과적으로 ‘Castle on the Hill is recommended since you have listened to Shape of You sung and written by Ed Sheeran’ 와 같은 설명이 가능해진다.

  • 본 논문의 기여는 다음과 같다.

    • explicit한 추론으로 추천의 이유를 설명할 수 있다.
    • end-to-end neural network 모델이 path의 의미들을 학습하고, 이를 추천에 통합한다.

Knowledge-aware Path Recurrent Network

Background

지식 그래프는 일종의 directed graph로, 노드는 엔티티 $E$이고 엣지는 관계 $R$이다. 지식 그래프는 다음과 같이 정의한다

$$ KG={(h,r,t)\:| \: h, t \in E, r \in R } $$

추천 시스템에서는 유저 $u$가 아이템 $i$과 상호작용 했을 때, 트리플렛 $\tau=(u, interact, i)$로 나타낸다.

Perferential Inference via Paths

지식 그래프 내의 경로는 유저와 아이템 사이의 직간접적 관계를 나타낸다. $e_1=u$이고 $e_L=i$라고 놓았을 때, 두 엔티티 사이의 경로는 아래와 같이 표현할 수 있다.

$$ p=[e_1 \xrightarrow{r_1} e_2 \xrightarrow{r_2} ... \xrightarrow{r_{L-1}} e_L] $$

지식 그래프를 이용한 추천 시스템에서는 이런 경로를 통해 설명 가능한 추천을 수행할 수 있다.

예를 들어,

$$ p_1=[Alice \xrightarrow{Interact} Shape\:of\:you \xrightarrow{SungBy} Ed\:Sheeran \xrightarrow{IsSingerOf} I\:See\:Fire] $$

여러 경로를 거쳐 $Alice$에서 $I\:See\:Fire$까지 이어지며, compositioinal semantics를 통해 추천 이유를 설명할 수도 있다.

$$ p_2=[Alice \xrightarrow{Interact} Shape\:of\:you \xrightarrow{InteractedBy} Tony \xrightarrow{Interact} I\:See\:Fire] $$

이런 식으로 CF 효과를 포착할 수도 있다.

Modeling

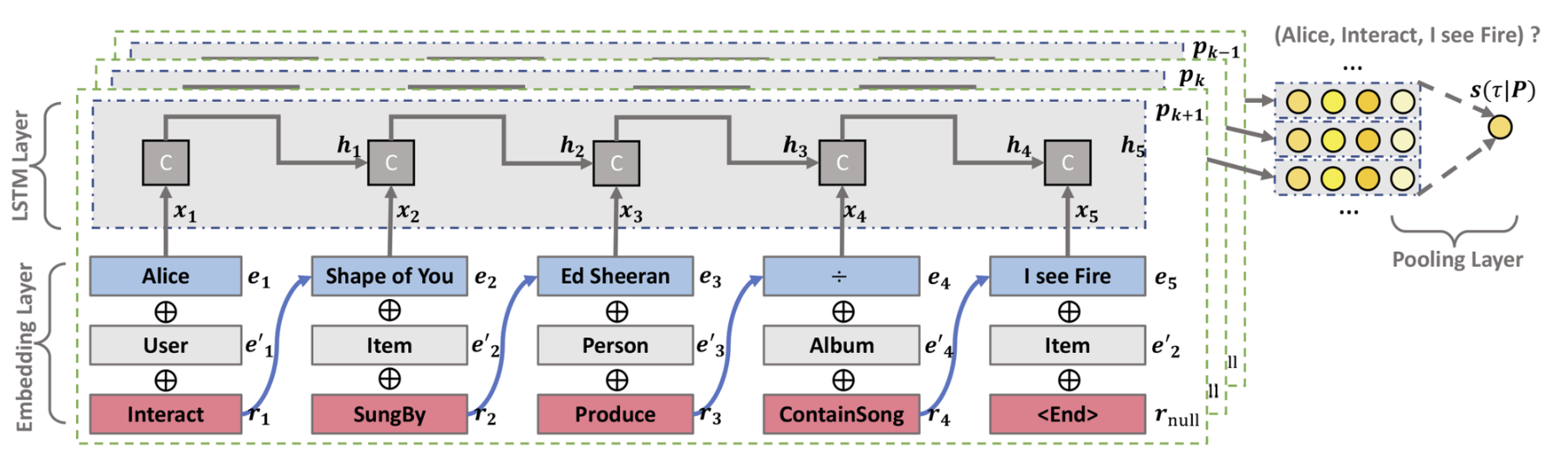
KPRN은 3가지의 주요 컴포넌트로 이루어져 있다.

Embedding layer

경로 $p_k$를 임베딩 벡터로 표현하는 레이어.

임베딩을 할 때는 엔티티의 구체적인 값 $e_l$, 엔티티의 타입 $e'_l$ + 관계 종류 $r_l$이 모두 반영된다.

이 레이어를 거쳐 경로 $p_k$는 set of embeddings $[\mathbf{e}_1, \mathbf{r}_1, \mathbf{e}_2, ..., \mathbf{r}_{L-1}, \mathbf{e}_L]$으로 나타낼 수 있다.

LSTM layer

Long-term sequential information을 활용하기 위해 LSTM을 쓴다.

각 path step에서, LSTM 레이어는 다음과 같은 인풋을 받고 hidden state를 계산한다.

• input vector: $\mathbf{x}_{l}=\mathbf{e}_{l} \oplus \mathbf{e'}_{l} \oplus \mathbf{r}_{l}$
  • 마지막 엔티티의 경우 null relation $r_L$을 패딩
  • 이 방식을 통해, 인풋 벡터는 sequential한 정보 뿐 아니라 semantic한 정보도 반영하게 된다

• hidden statses: $\mathbf{h}_{l-1}$

  • 이전 단계로부터 받은 hidden state

  • 다음 hidden state는 아래와 같이 계산합니다 ($\mathbf{c}$는 cell state, $\mathbf{z}$는 information transform module, $\mathbf{i}, \mathbf{o}, \mathbf{f}$는 각각 input, output, forget gate)

  • $$ \begin{align} \mathbf{z}_l &= tanh(\mathbf{W}_z\mathbf{x}_l+\mathbf{W}_h\mathbf{h}_{l-1}+\mathbf{b}_z) \\\ \mathbf{f}_l &= \sigma(\mathbf{W}_f\mathbf{x}_l+\mathbf{W}_h\mathbf{h}_{l-1}+\mathbf{b}_f) \\\ \mathbf{i}_l &= \sigma(\mathbf{W}_i\mathbf{x}_l+\mathbf{W}_h\mathbf{h}_{l-1}+\mathbf{b}_i) \\\ \mathbf{o}_l &= \sigma(\mathbf{W}_o\mathbf{x}_l+\mathbf{W}_h\mathbf{h}_{l-1}+\mathbf{b}_o) \\\ \mathbf{c}_l &= \mathbf{f}_l \odot \mathbf{c}_{l-1}+\mathbf{i}_l \odot \mathbf{z}_l \\\ \mathbf{h}_l &= \mathbf{o}_l \odot tanh(\mathbf{c}_l) \end{align} $$

  • memory state 덕분에 마지막 hidden state $\mathbf{h}_L$는 전체 경로 $p_k$의 정보를 담고 있다.

이 과정이 끝나고 나면 경로 $p_k$의 representation을 얻게 된다.

이후 어떤 트리플렛 $\tau=(u, interact, i)$의 예상 점수를 구할 때는 두 개의 fully connected layer를 이용한다.

$$ s(\tau|\mathbf{p}_k)=\mathbf{W_2}^\intercal ReLU(\mathbf{W_1}^\intercal \mathbf{p}_k) $$

Pooling layer

유저 $u$와 아이템 $i$를 연결하는 $K$개의 경로로부터 얻은 점수 $S={s_1, s_2, ..., s_K}$가 있다고 할 때, 최종 점수는 다음과 같은 weighted pooling으로 정해진다.

$$ \hat{y}_{ui}=\sigma \left( log \left[ \sum_{k=1}^{K}{exp \left( \frac{s_k}{\gamma} \right)}\right] \right) $$

단순한 평균 대신 이런 방식을 쓰면 몇 가지 장점이 있다.

• 각 경로의 중요성을 구분할 수 있음
• $\gamma$ 값에 따라 유연한 추천이 가능함. 예를 들어, $\gamma \rightarrow 0$이면 max pooling, $\gamma \rightarrow \infty$면 mean pooling에 가까워짐

Learning

유저-아이템 상호작용을 이진 분류 문제로 보고 학습.

$$ L=-\sum_{(u,i)\in O^{+}}{log \: \hat{y}_{ui}} + \sum_{(u,j)\in O^{-}}{log \:(1-\hat{y}_{uj})} $$

Experiments

Settings

Dataset Description

본 논문에서는 두 가지 데이터셋으로 KPRN을 실험

1. MovieLens 1M과 IMDb 데이터셋 함께 사용 (이하 MI)
2. KKBox라는 음악 스트리밍 데이터셋

하나의 positive sample마다 같은 유저의 negative sample 4개를 샘플링하여 사용

Path Extraction

현실적으로 네트워크 상의 모든 경로를 뽑아내 사용하는 것은 비효율적.

본 연구에서는 길이가 6 이내인 유저-아이템 경로만 뽑아내서 사용.

Evaluation Metrics

평가에는 두 가지 지표를 사용함.

• hit@K: 상위 K개의 추천에 relevant item이 몇 개나 있는지
• ndcg@K: 상위 K개의 추천 중에서, relevant item의 순위에 가중치를 두어 계산하는 점수

K는 1~15의 값으로 바꿔가면서 실험.

Baselines

비교 대상으로는 네 가지 모델을 사용함

• MF: 유저-아이템의 상호작용 정보만 사용하는 factorization 모델
• NFM: 유저의 아이템 이력을 유저 피처로 사용하는 factorization 모델
• CKE: 지식 그래프를 활용한 추천 시스템 (Embedding-based)
• FMG: 지식 그래프를 활용한 추천 시스템 (Path-based)

Performance Comparison

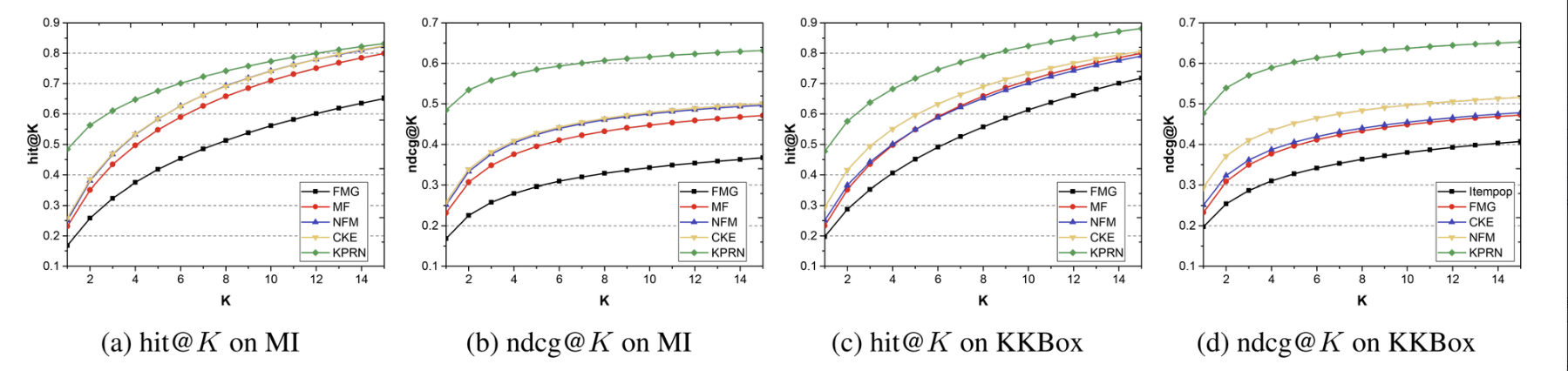
KPRN이 좋으니까 논문이 나왔겠죠…?

• NFM은 MF보다 성능이 좋음.
• CF 기반 방법들(MF, NFM)과 비교해봤을 때, CKE는 sparse한 데이터셋에서 강점을 보임. 이는 지식 그래프를 활용한 방식이 sparsity 문제를 다루는 데 효과적이라는 것을 보여줌. 반면 dense한 영화 데이터셋에서는 성능이 큰 차이 없음
• 반면 FMG는 두 데이터셋 모두 성능이 좋지 않음. 메타 그래프를 이용하는 방식은 유저-아이템 연결성을 충분히 활용하지 못하는 것으로 보임
• KPRN은 CKE는 물론이고 다른 모델을 압도함.

Study of KPRN

Relation modeling의 역할

relation modeling을 하지 않는 KPRN-r 모델을 만들어 비교. (즉, input vector $\mathbf{x}_{l}=\mathbf{e}_{l} \oplus \mathbf{e'}_{l}$)

• 두 데이터셋 모두 KPRN-r의 성능이 KPRN보다 떨어짐
• 성능이 떨어진 정도는 KKBox(0.70%)보다 MI(6.45%) 데이터셋에서 더 크다. density의 영향일 수 있음

Weighted pooling에서 $\gamma$의 영향

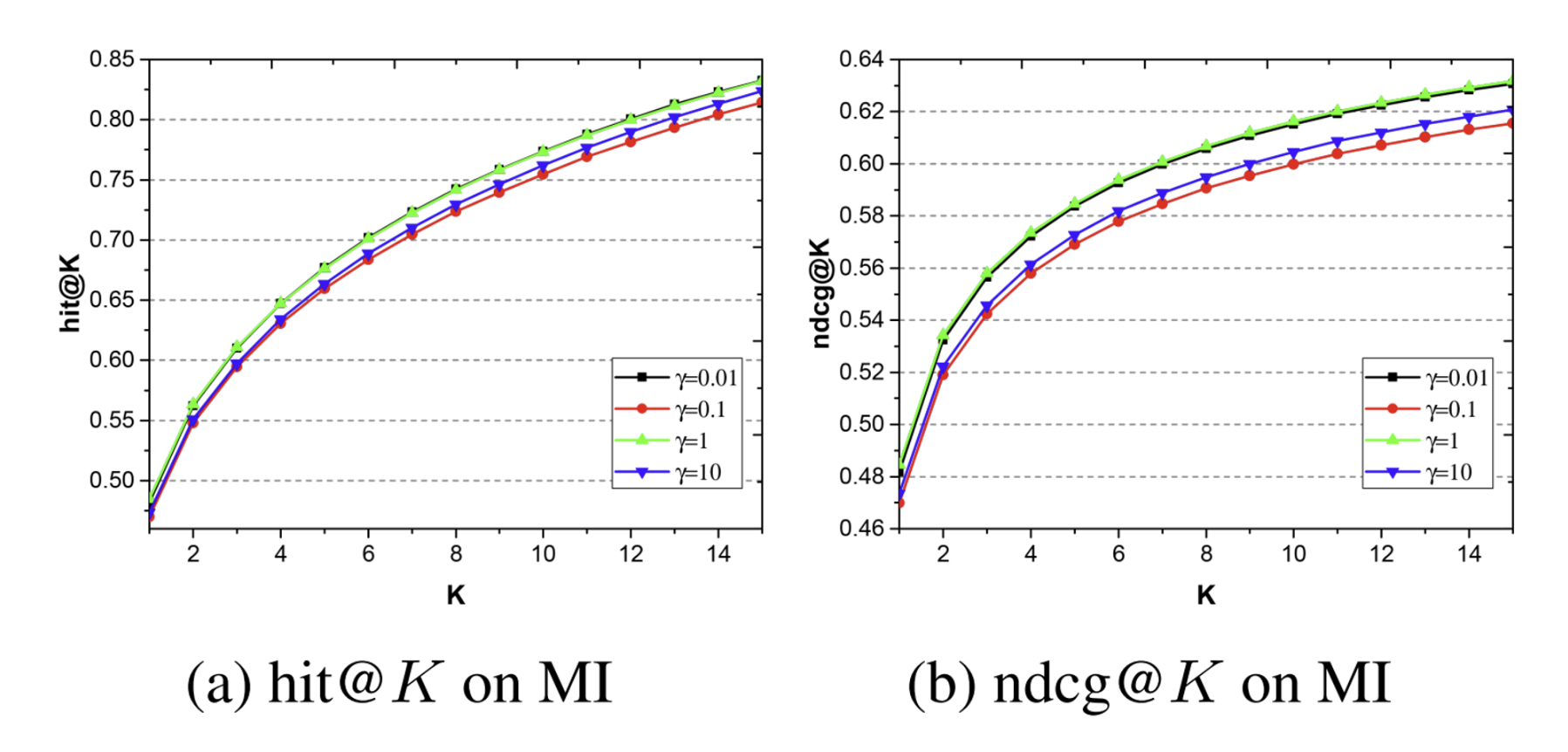
$\gamma$의 값을 [0.01, 0.1, 1, 10]으로 바꿔가면서 실험.

• $\gamma$가 1에서 0.1로 줄어들 때 (max-pooling에 가까워짐) 성능이 떨어짐
• $\gamma$가 1에서 10으로 늘어날 때 성능이 떨어짐

---