Neural graph collaborative filtering

2023-04-02

📄 paper : Neural graph collaborative filtering ↗

---

레퍼런스 / 학습 자료

🔗 graph Laplacian norm 자세한 설명 ↗

🔗 https://velog.io/@yoonbee7/논문-Neural-Graph-Collaborative-Filtering(논문 관련 설명) ↗

---

2. METHODOLOGY

2. 1 Embedding Layer

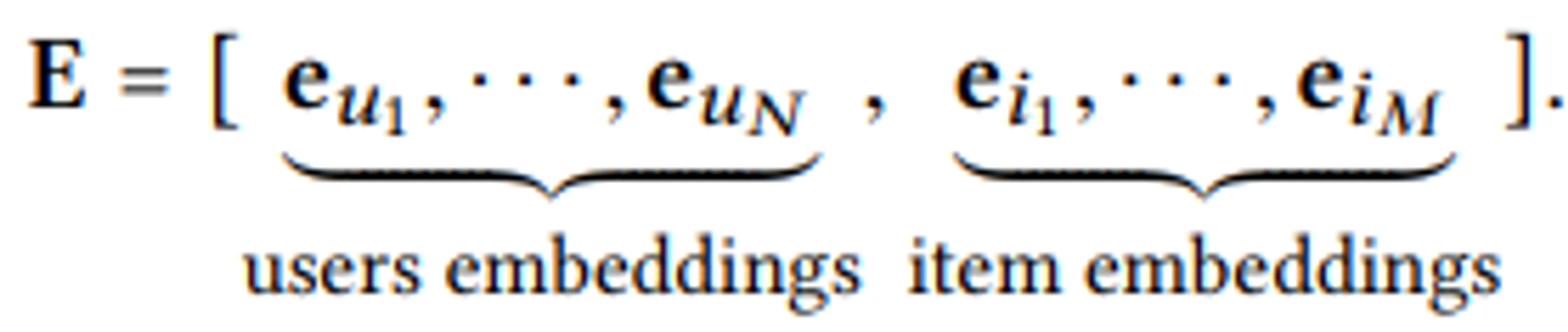
user 와 item 임베딩을 column 벡터형태로 하나의 parameter matrix인 E로 표현.

기존의 MF와 NCF 방법론에서는 임베딩들을 interaction layer에 직접 연결하여 prediction score를 계산.

But, NGCF는 유저와 아이템 간의 interaction graph를 활용하여 임베딩 propagation 통해 값들을 개선.

이러한 임베딩을 refine하는 과정을 통해 임베딩에서 collaborative signal 명시적으로 주입하여 효과적인 임베딩이 가능하게 함.

2. 2 Embedding Propagation Layers

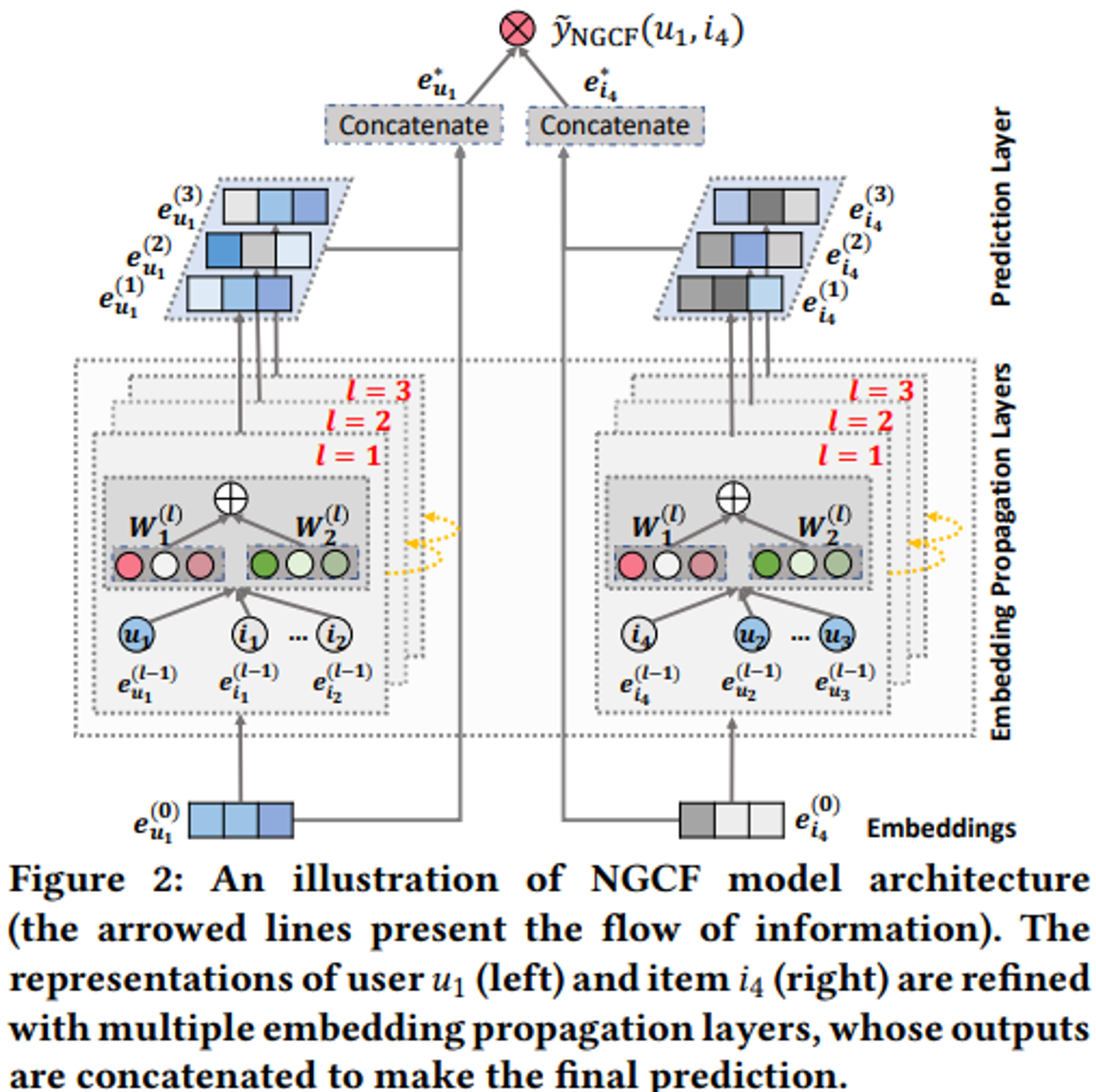
그래프 구조를 통해 CF signal을 캡쳐하기 위해서 GNN의 message-passing architecture 를 구축해서 user, item 임베딩을 refine 함.

2. 2. 1 First-order propagation

interacted item들은 user들의 선호도에 대한 direct한 증거를 제공. → item들을 소비한 user들을 그 item들의 feature로서 사용할 수 있고 유사도를 구하는데 활용됨.

그러한 연결된 user와 item 간의 embedding propagation 수행할 때 Message Construction 과 Message Aggregation이 쓰임.

Message Construction

연결된 user와 item 쌍 ($u, i$)에 대해 $u$에서 $i$로 전달되는 메세지를 다음과 같이 정의

$m_{u←i}=f(e_i,e_u,p_{ui})$, $m_{u←i} = \frac{1}{\sqrt{|N_u||N_i|}}(W_1e_i+W_2(e_i\odot e_u))$

$m_{u←i}$ : 전파되는 정보를 나타내는 메시지 임베딩

$W_1, W_2\in \mathbb{R}^{d'\times d}$ 은 학습가능한 weight matrix, $d'$는 transformation size

$e_i$만 고려하는 GCN과 달리 NGCF는 $W_2(e_i\odot e_u)$ 식을 통해 $e_i$와 $e_u$를 element-wise 하여 상호작용을 전달해줌

→ 비슷한 item으로부터 더 많은 메세지를 전달

GCN에 따르면 $p_{ui}$는 graph Laplacian norm($\frac{1}{\sqrt{|N_u||N_i|}}$)

• Graph Laplacian norm 이란?

  

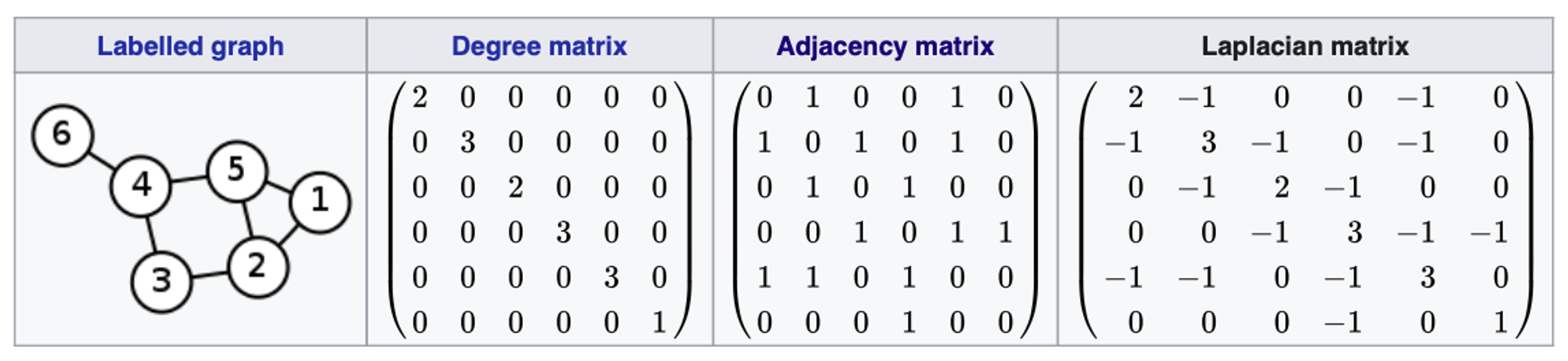
  Symmetric normalized laplacian matrix → 말 그대로 라플라시안 행렬을 정규화한 것. 차수 정보(degree)가 모두 1로 통일

  

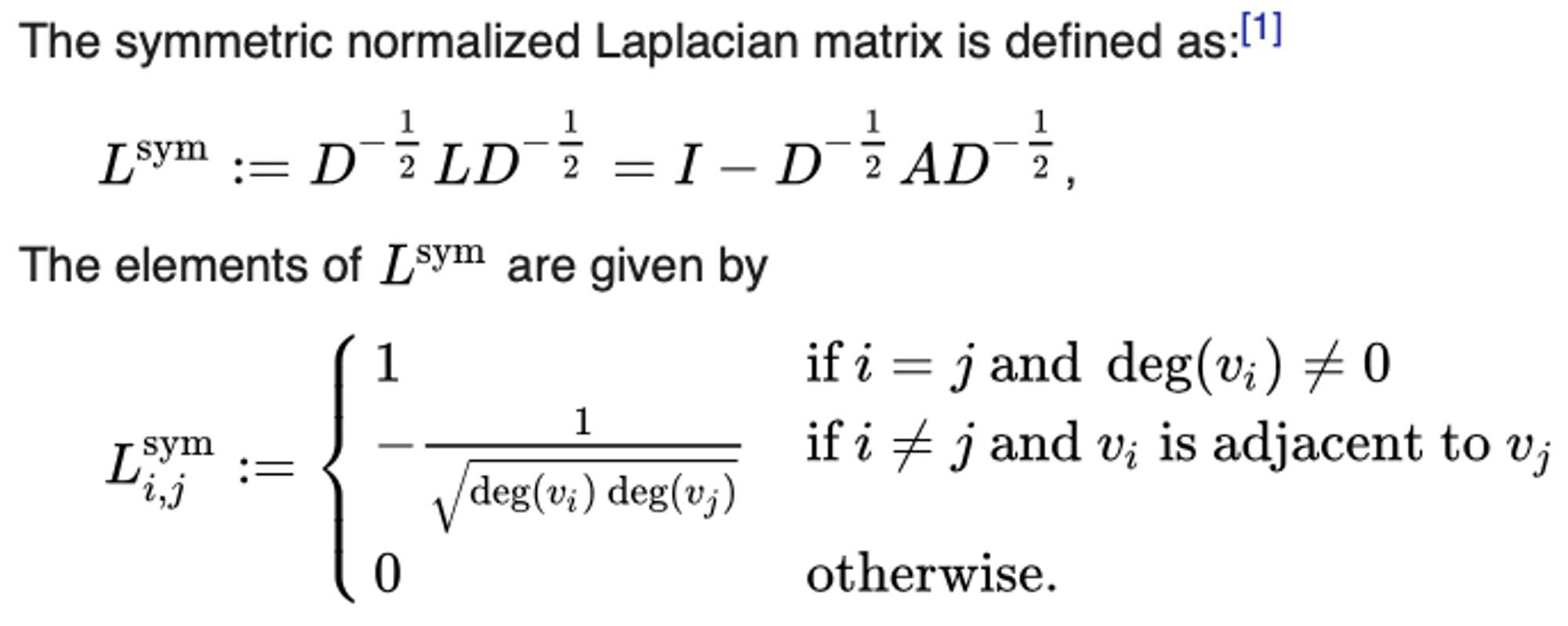
즉, $p_{ui}$는 item을 소비한 user의 수와 user가 평가한 item의 수의 영향을 반영시키는 역할.

Message Aggregation

construction된 메세지들을 aggregation하는 과정

Aggregation function → $e^{(1)}_u=\text{LeakyReLU}(m_{u←u}+\sum_{i \in N_u}m_{u←i})$

$u$의 이웃 노드들에서 전파된 메세지들을 결합하여 첫번째 embedding propagation layer를 통과한 결과 $m_{u←u}$를 통해 유저가 가지고 있는 original feature 정보를 유지

이 때 $m_{u←u}=W_1e_u$

item 에 대한 임베딩 값($e_i$) 역시 위와 같은 방법으로 진행.

2. 2. 2 High-order Propagation

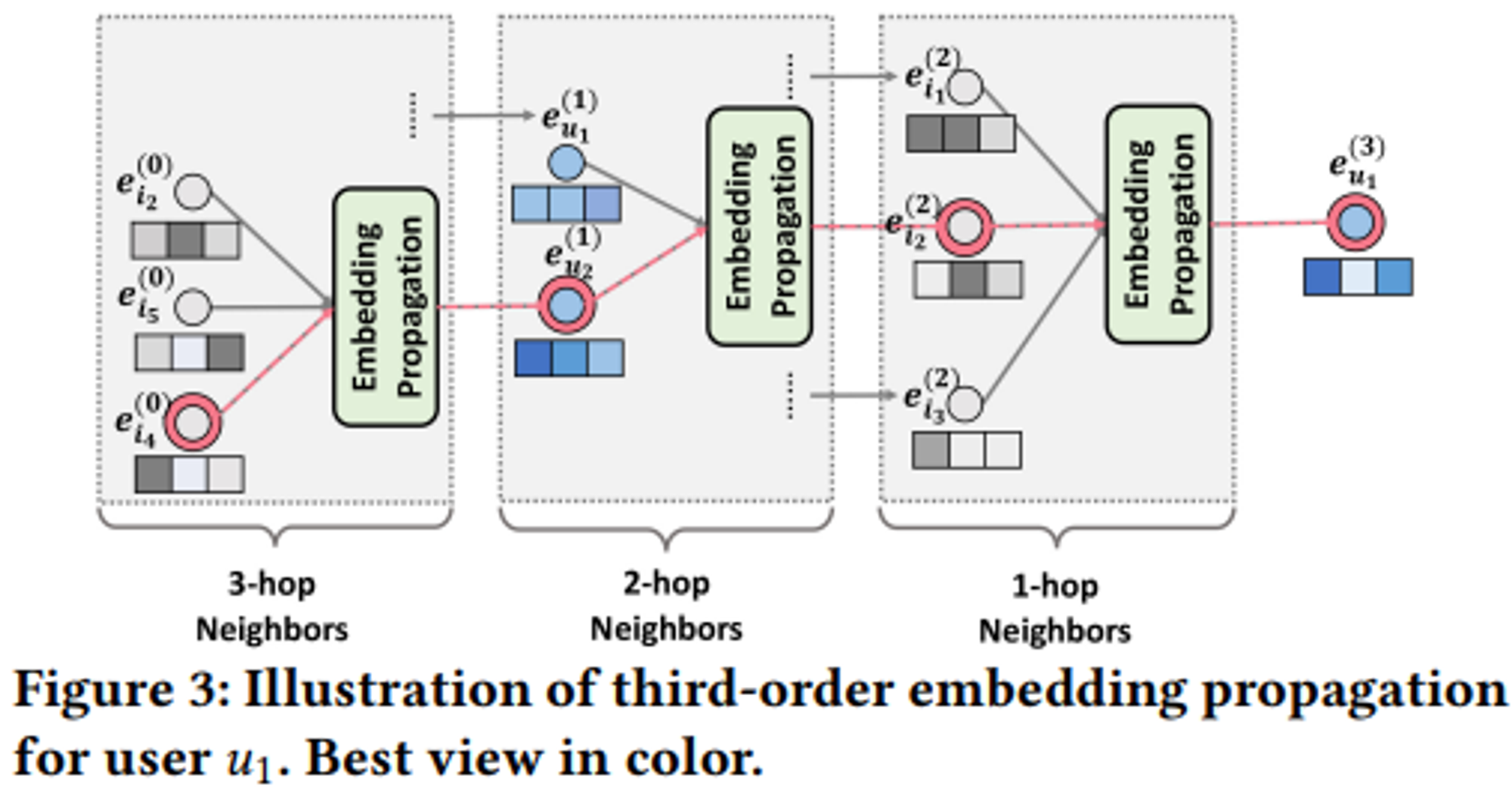
이러한 Embedding propagation layer가 $l$개 만큼 쌓이면 high-order propagation이 되고 $l$ 거리만큼 떨어진 이웃의 메세지 정보를 활용함.

$e^{(l)}_u=\text{LeakyReLU}(m^{l}_{u←u}+\sum_{i \in N_u}m^{l}_{u←i})$

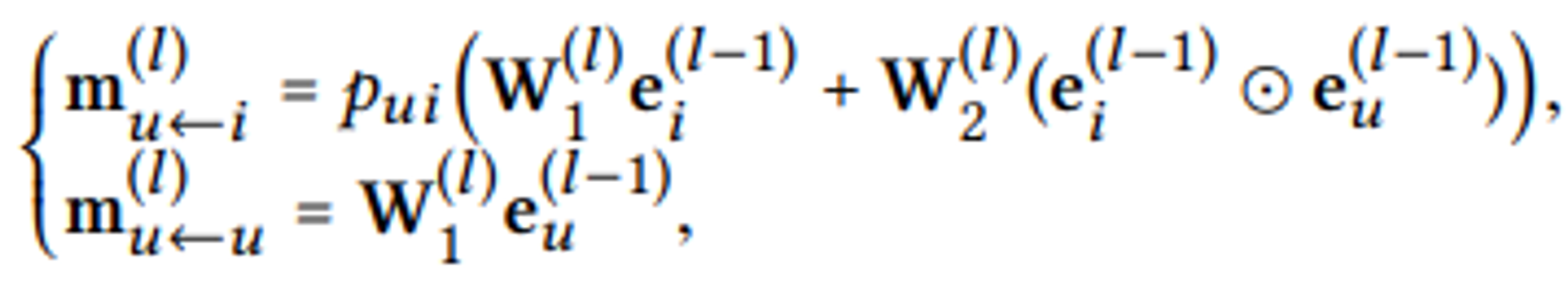
Propagation Rule in Matrix Form

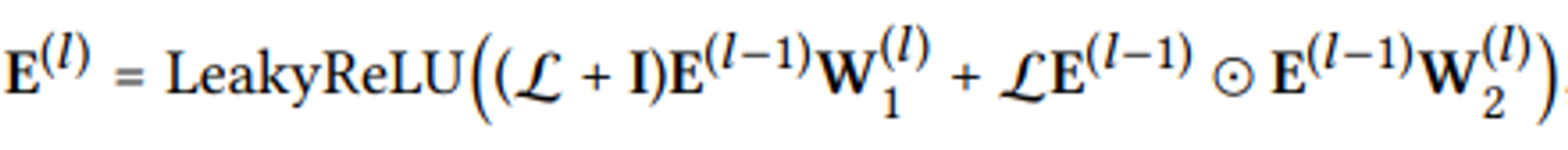
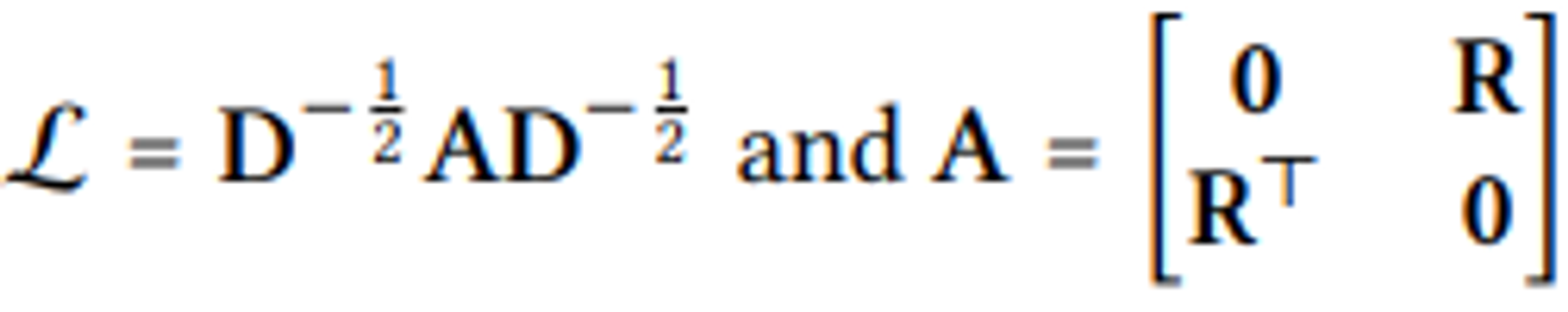
이러한 matrix 형태로 모든 user와 item에 대한 표현을 동시에 업데이트함.

2. 3 Model Prediction

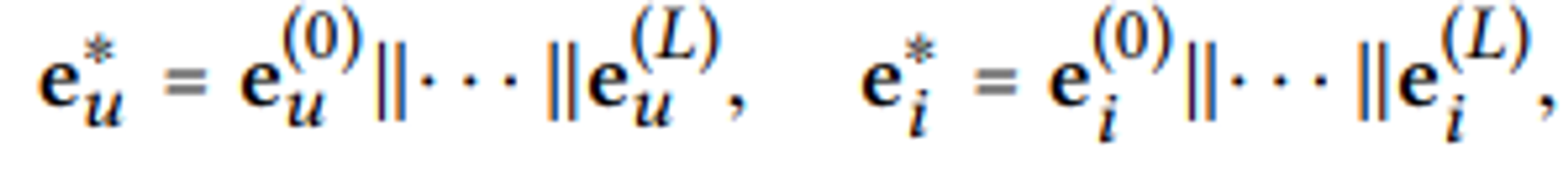
Embedding propagation layer 과정이 종료되고 $L$번째 layer까지 임베딩 벡터를 형성했으면 user와 item 별로 각각 concatenate 하여 최종 Embedding을 구성.

user와 item의 최종 임베딩 벡터 내적하여 선호도 추정

$$\hat{y}_{NGCF}(u,i)={e^*_u}^\intercal e^*_i$$

2. 4 Optimization

loss function은 BPR LOSS를 통해 최적화

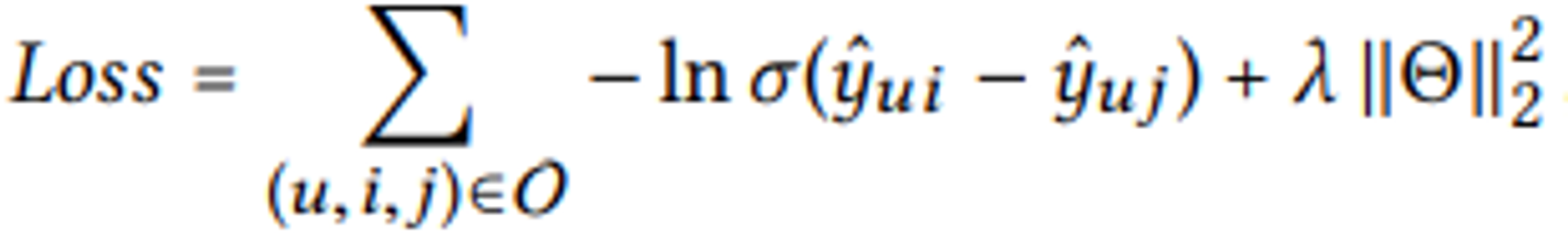
$O = {(u, i, j)|(u, i) \in \mathbf{R}^+, (u,i) \in \mathbf{R}^-}$ → 관측된 것($\mathbf{R}^+$)과 관측되지 않은($\mathbf{R}^-$) interaction을 모두 포함한 training data

$\Theta = {E, {W_1^{\left( l \right)}, W_2^{\left( l \right)}}_{l=1}^L}$ → 모든 학습가능한 파라미터($L_2$)

Node Dropout

random selection으로 특정 user or item(노드) 에서 보내는 모든 메세지 삭제(노드와 메세지 전부 삭제)

→ 특정 user or item의 영향을 줄여줌

Message Dropout

random selection으로 노드는 그대로 두고 message만 삭제

→ user와 item 사이의 single connection 표현에 더 많은 robustness 부여.

4. EXPERIMENTS

RQ1

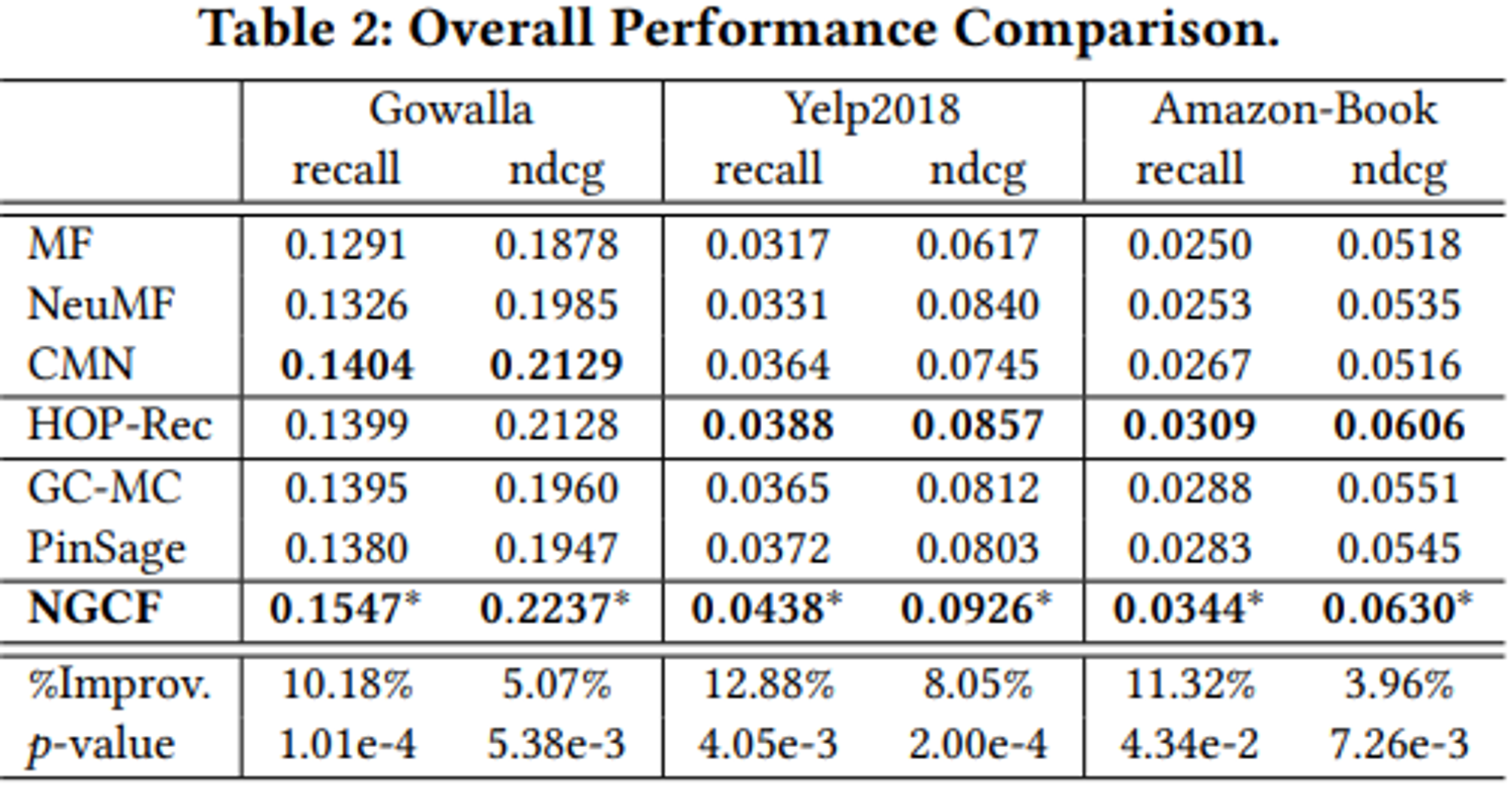
RQ2

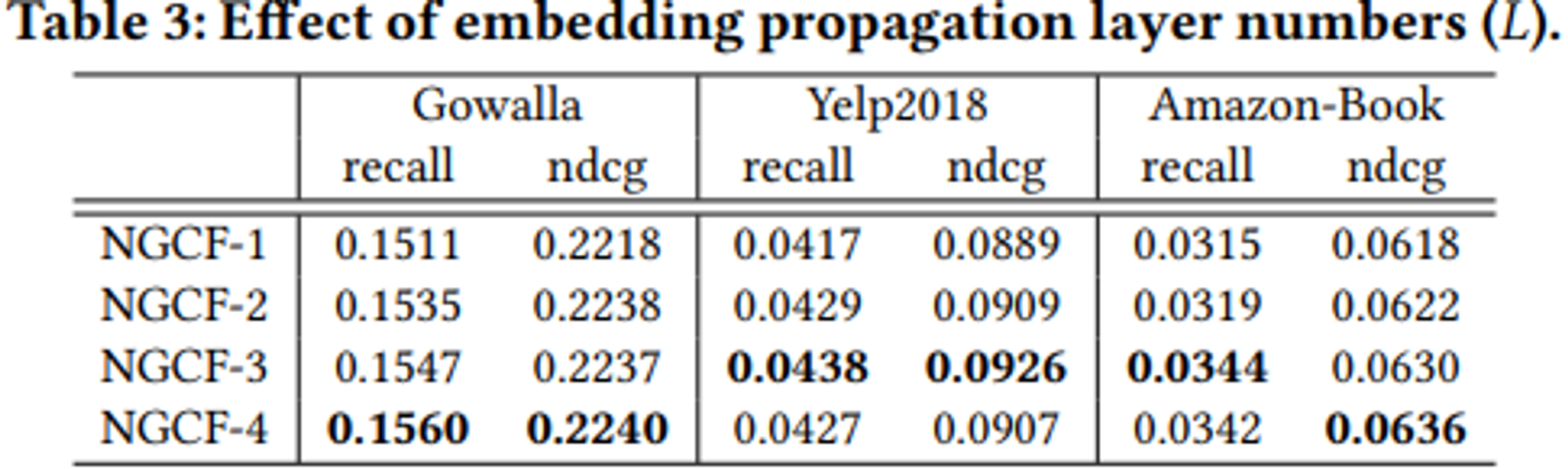
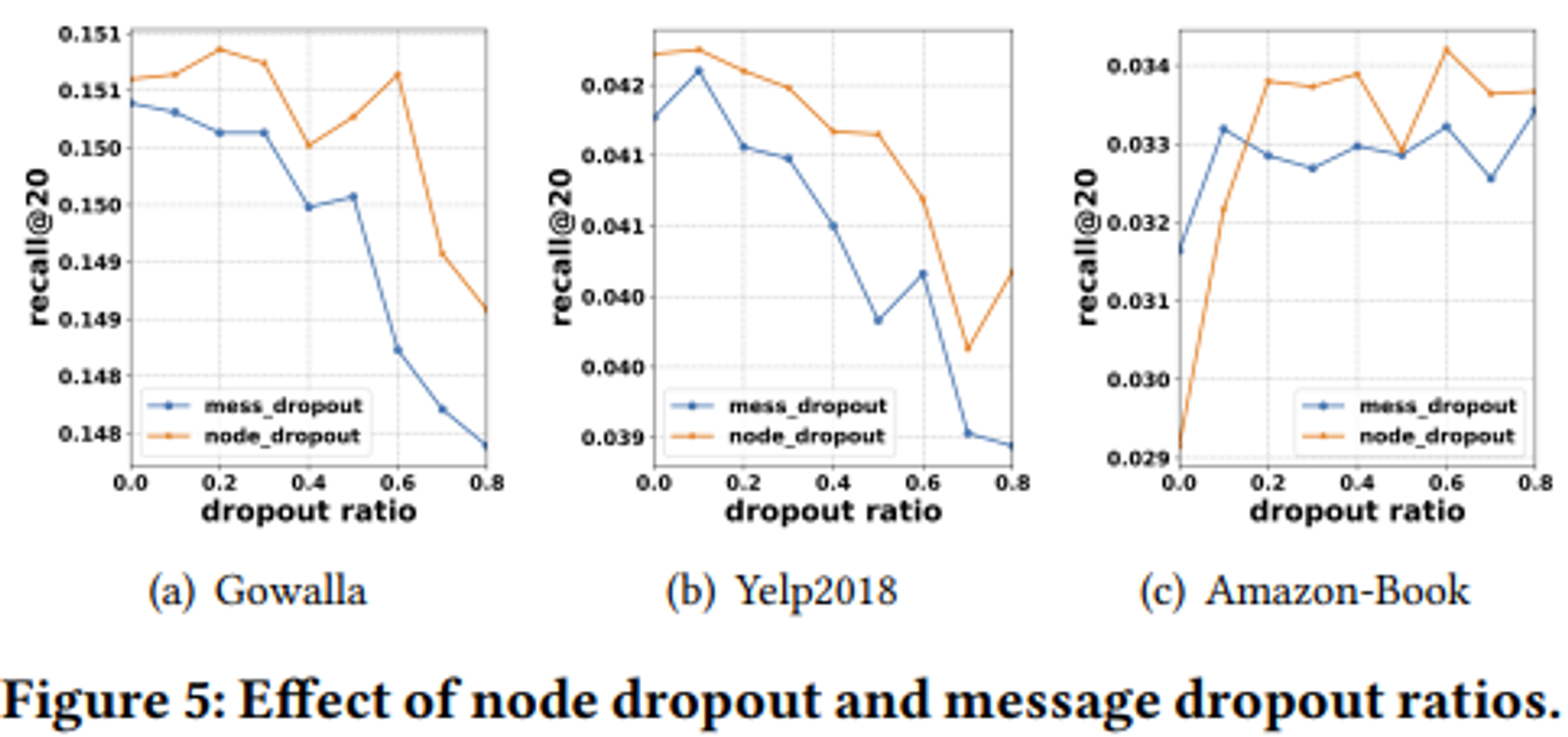
RQ3

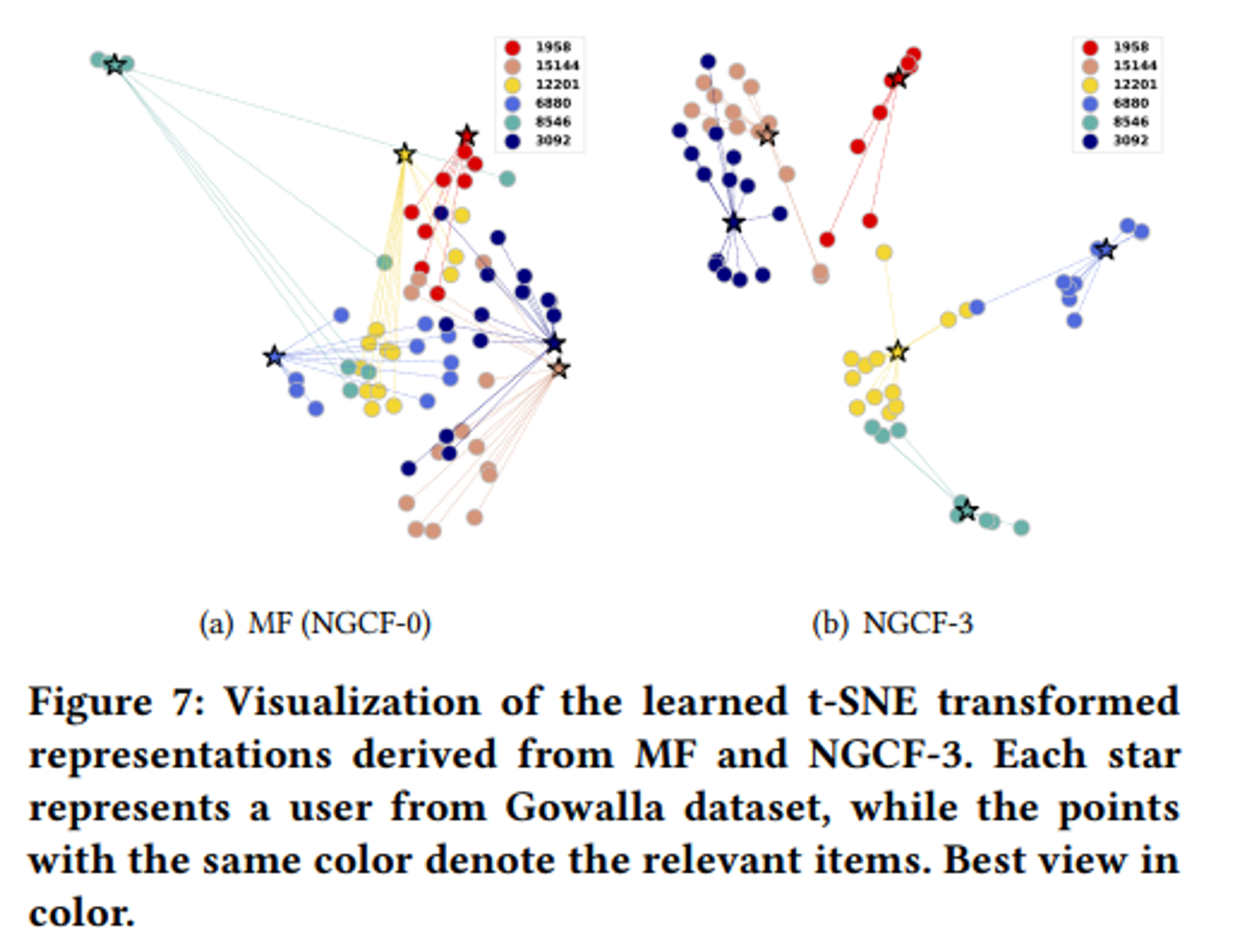
5. Conclusion and Future work

기존의 Embedding 방법과 달리 Embedding propagation layer 쌓는 방식을 제안함.

Message construction과 Message aggregation 으로 High order connectivity를 모델링하여 collaborative signal을 캡쳐하는 그래프 기반 추천 프레임워크 제안.

추후 임베딩 전파 과정에서 이웃에 대한 변수 가중치와 다른 순서의 연결성을 학습하기 위해 attention mechanism 을 통합하여 NGCF를 개선할 것을 기대, 머신러닝 생태계를 건강하게 만들어주셔서 감사합니다! 이 지식이 확산되어 더 큰 가치를 형성할 것입니다!

---