Self-Attentive Sequential Recommendation

2023-03-26

SASRec

📄 paper : Self-Attentive Sequential Recommendation ↗

---

III. METHODOLOGY

유저의 행동 시퀀스 $\mathcal{S}^u = (\mathcal{S}_1^u, \mathcal{S}_2^u, \cdots, \mathcal{S}_{|\mathcal{S}^u|}^u)$가 있고, 다음 아이템을 예측해야한다!

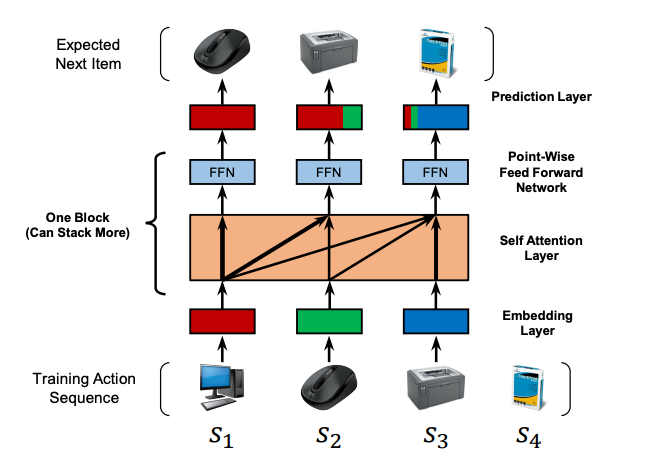
학습 시, $t$ 시점에서는 이전의 $t$개의 아이템에 기반하여 다음 아이템을 예측한다. 사진에서 볼 수 있듯이, 모델의 인풋은 $(\mathcal{S}_1^u, \mathcal{S}_2^u, \cdots, \mathcal{S}_{|\mathcal{S}^u|-1}^u)$이, 아웃풋은 $(\mathcal{S}_2^u, \mathcal{S}_3^u, \cdots, \mathcal{S}_{|\mathcal{S}^u|}^u)$(shift됨)가 되는 것이다.

A. Embedding Layer

학습 데이터 $(\mathcal{S}_1^u, \mathcal{S}_2^u, \cdots, \mathcal{S}_{|\mathcal{S}^u|-1}^u)$를 고정 길이의 $s = (s_1, s_2, \cdots, s_n)$으로 변환한다. $n$은 모델의 maximum length를 나타낸다.

만약 시퀀스가 $n$보다 크면, 최근의 $n$개만 사용한다. 만약 시퀀스가 $n$보다 짧으면, 왼쪽을 padding item으로 채운다.

임베딩 행렬 $\mathbf{M} \in \mathbb{R}^{|\mathcal{I}| \times d}$를 만든다. $d$는 차원을 의미한다.

인풋 임베딩 행렬은 $\mathbf{E}=\mathbb{R}^{n \times d}$가 될 것이다. 인풋 시퀀스 길이가 $n$이니까!

Positional Embedding : 셀프어텐션은 이전 아이템의 위치를 알지 못한다. Positional embedding $\mathbf{P} = \mathbb{R}^{n \times d}$를 인풋 임베딩에 더해준다.

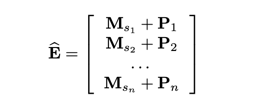
B. Self-Attention Block

아이템 개수 : $\mathcal{I}$

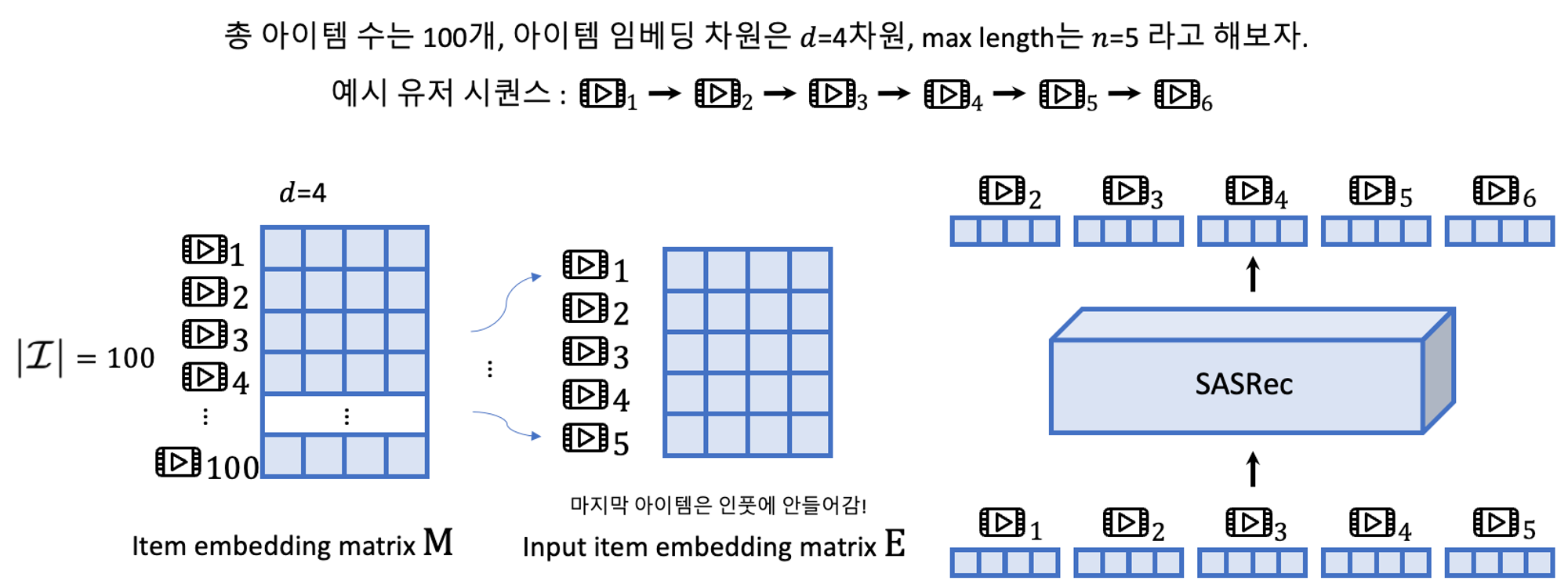
(실제로는 50차원을 사용함!)

어텐션 복습. scaled dot-product attention은 다음과 같이 정의된다.

$$ \text{Attention}(\mathbf{Q}, \mathbf{K}, \mathbf{V}) = \text{softmax}\left(\frac{\mathbf{Q}\mathbf{K}^T}{\sqrt{d}}\right)\mathbf{V} $$

$\mathbf{Q}$는 query를, $\mathbf{K}$는 key를, $\mathbf{V}$는 value를 나타낸다.

어텐션 함수는 주어진 '쿼리(Query)'에 대해서 모든 '키(Key)'와의 유사도를 각각 구합니다. 그리고 구해낸 이 유사도를 키와 맵핑되어있는 각각의 '값(Value)'에 반영해줍니다. - 딥 러닝을 이용한 자연어 처리 입문

NLP에서는 $K$=$V$를 encoder의 hidden layer로, Q를 decoder의 hidden layer로 사용한다.

최근(논문이 발표되었던 2018년 즈음)에는, $K$=$V$=$Q$인 self-attention이 제안되었음.

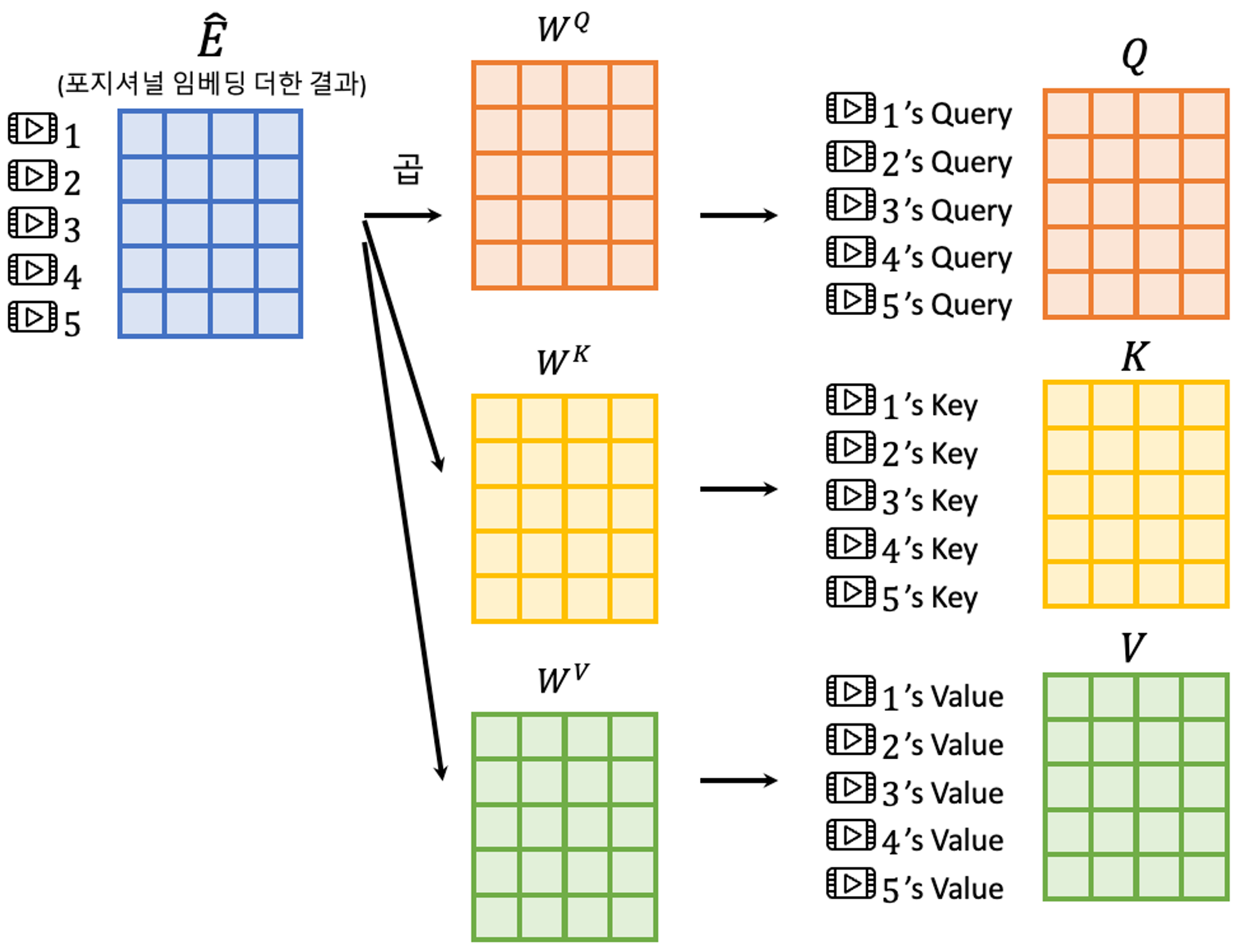
여기서는 $\hat{\mathbf{E}}$를 $\mathbf{W}^Q$, $\mathbf{W}^K$, $\mathbf{W}^V$로 각각 사영시킨 $\hat{\mathbf{E}}\mathbf{W}^Q$,$\hat{\mathbf{E}}\mathbf{W}^K$, $\hat{\mathbf{E}}\mathbf{W}^V$를 사용한다.

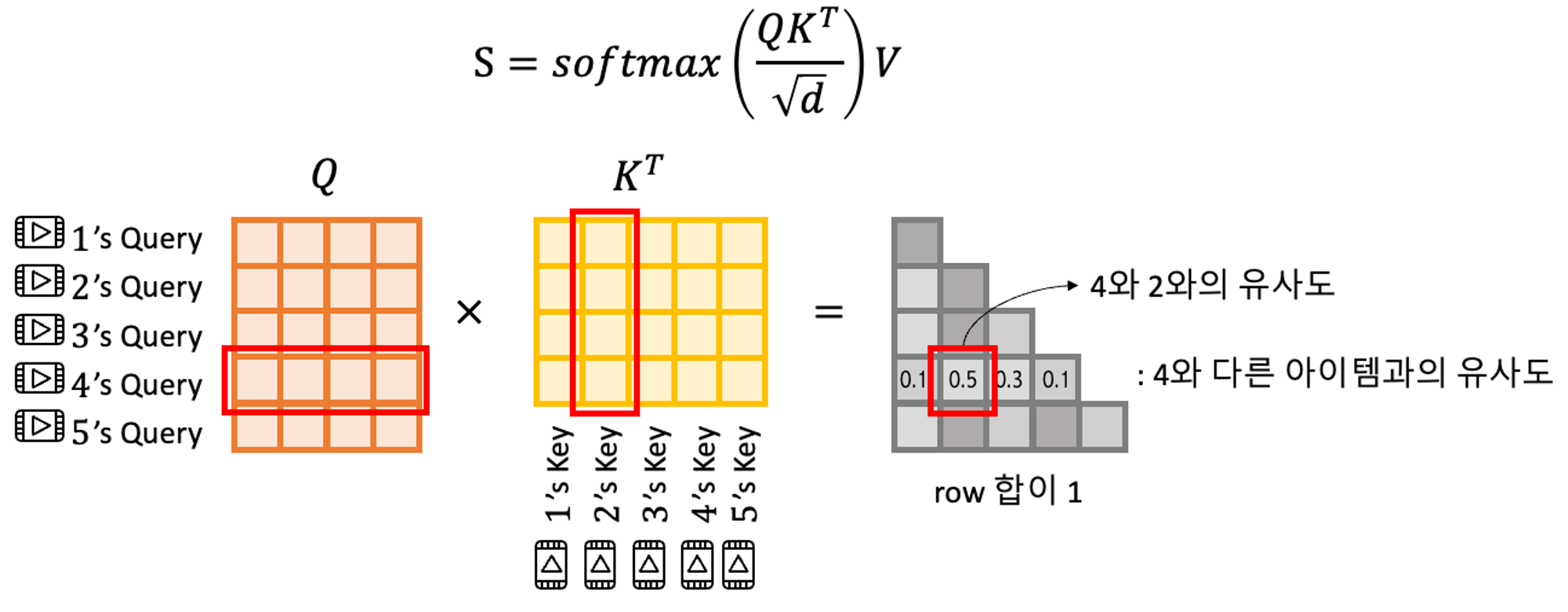
Casuality(인과관계) : lower triangle만 사용하는 이유

시퀀스의 특성을 생각해보자. 모델은 $t+1$번째 아이템을 예측하기 위해서 오직 앞에 놓인 $t$개의 아이템들을 고려해야만 한다. 모델이 해서는 안되는 행동(?)은 $t+1$번째 아이템을 예측하기 위해 $t+2$번째 아이템을 고려대상에 포함시키는 것이다.

그러나 셀프어텐션의 결과를 보면, 예를 들어 2번째 아웃풋 $\mathbf{S}_2$는 그 뒤에 나오는 3, 4번째 아이템의 임베딩 정보를 포함하고 있게 된다. 그러므로, 어텐션을 수정하여, $j>i$인 $\mathbf{Q}_i$와 $\mathbf{K}_j$사이의 모든 연결을 금지시킨다.

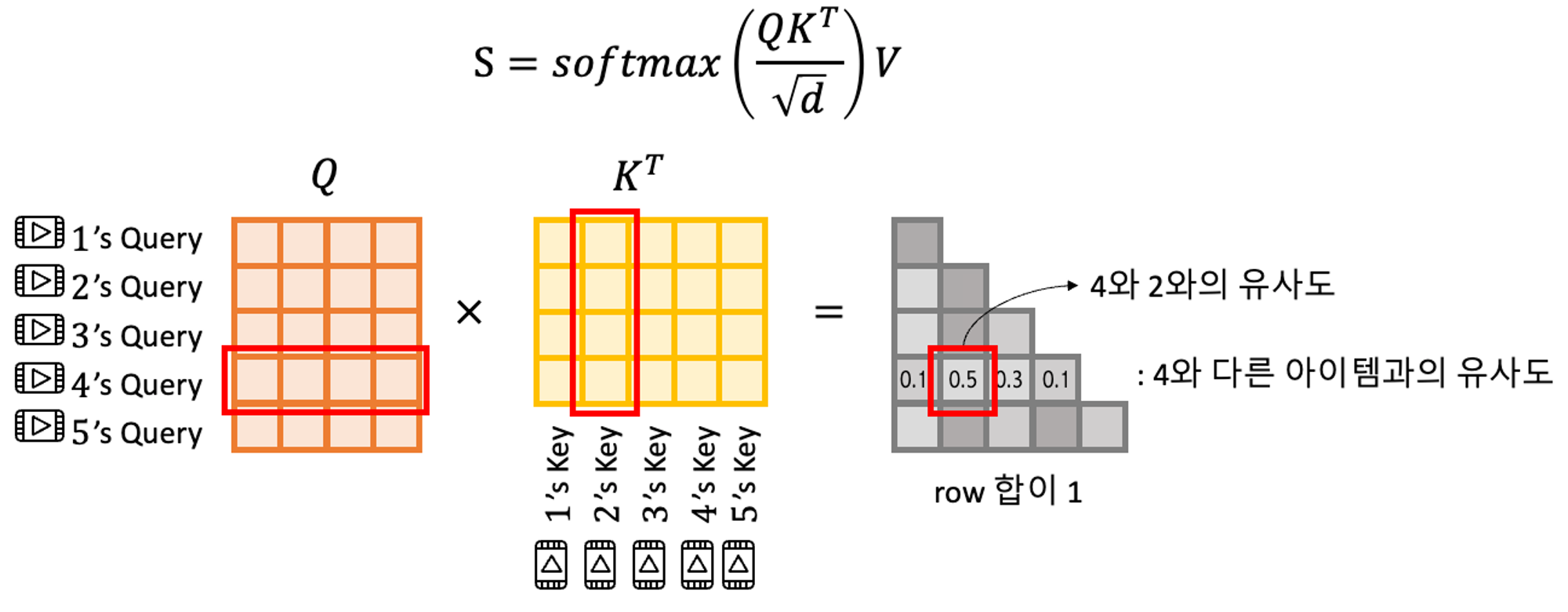
Point-Wise Feed-Forward Network

$$ \begin{align} \mathbf{F}_i &= \text{FFN}(\mathbf{S}_i) \\\ &= \text{ReLU}(\mathbf{S}_i \mathbf{W}^{(1)}+\mathbf{b}^{(1)})\mathbf{W}^{(2)} + \mathbf{b}^{(2)} \end{align} $$

$\mathbf{W}^{(1)}, \mathbf{W}^{(2)}$는 $d \times d$ (즉 우리 예시에서는 4X4)형태의 행렬이며, $\mathbf{b}^{(1)}$, $\mathbf{b}^{(2)}$는 $d$차원 벡터이다.

셀프어텐션이 이전의 모든 아이템의 임베딩을 선택적 결합을 시킬 순 있었지만, 이 결합은 궁극적으론 linear 모델이다. 그래서 여기서는 모델에게 비선형성을 주기 위해 2개의 point-wise feed-forward network를 모든 $\mathbf{S}_i$에게 파라미터를 공유하여 적용한다. $\mathbf{S}_i$와 $\mathbf{S}_j$ ($i \ne j$)사이에 상호작용은 없다. 뒤에서 앞의 아이템을 예측하는 information leak을 막기 위함이다.

C. Stacking Self-Attention Blocks

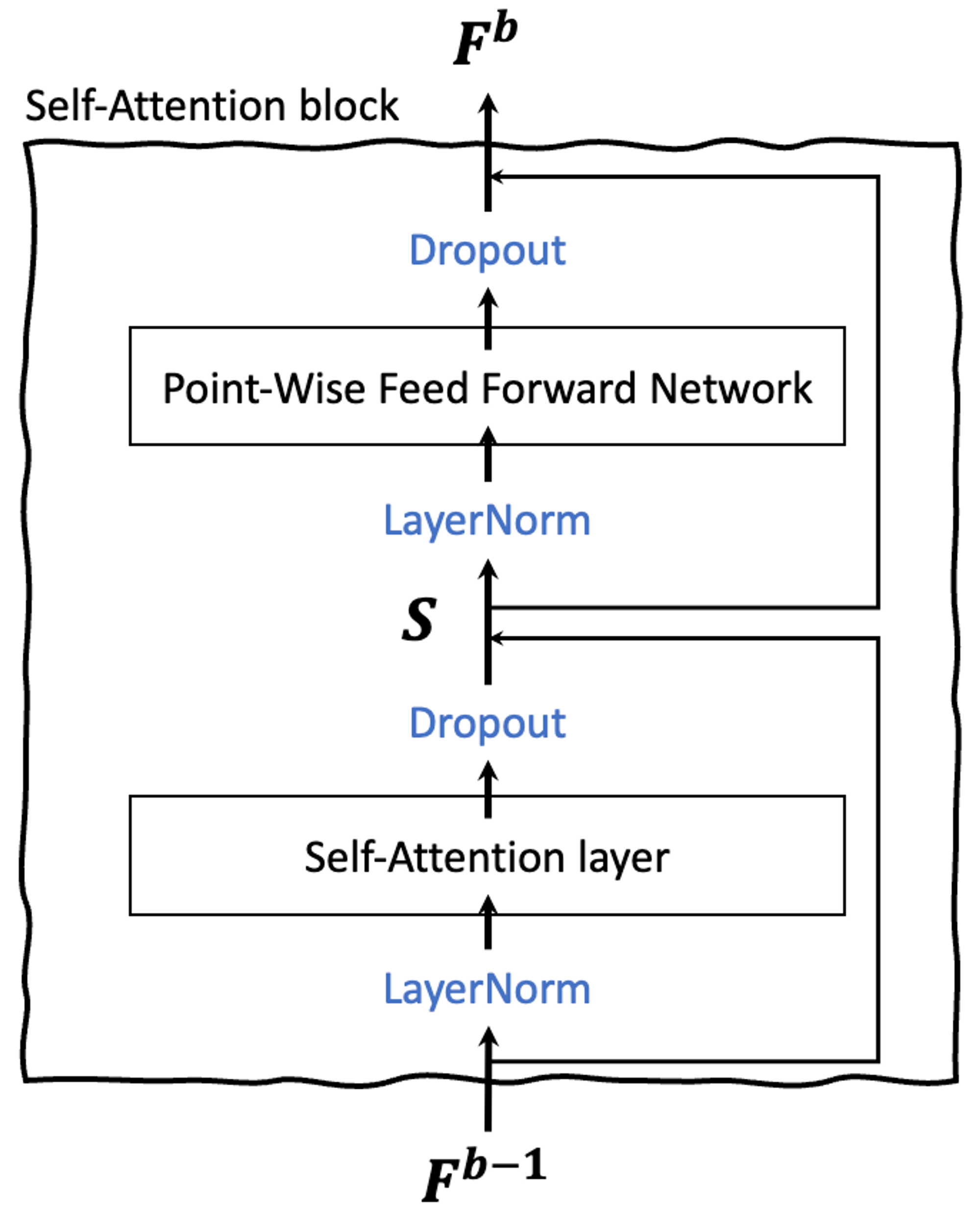
더욱 복잡한 아이템 사이의 transition을 학습해보자. 어떻게? Self-attention 블록(FFN 포함)을 더 쌓아보자!!

2번째 블록부터는 다음과 같이 정의된다! $b$($b > 1$)번째 블록은,

$$ \begin{align} \mathbf{S}^{(b)}&=\text{Self Attention Block}(\mathbf{F}^{(b-1)}) \\ \mathbf{F}_i^{(b)} &= \text{FFN}(\mathbf{S}_i^{(b)}), \;\;\; \forall i \in \{ 1, 2, ..., n \} \end{align} $$

$b-1$번째 $\mathbf{F}$를 받아 셀프어텐션과 FFN을 적용시킨다!! 참고로 첫 번째 블록은 $\mathbf{S}^{(1)}=\mathbf{S}, \mathbf{F}^{(1)}=\mathbf{F}$이다.

무조건 블록을 많이 쌓는것이 좋을까? 그럼 문제점도 있다.

1) 모델 capacity가 커져(파라미터가 많아져서) 오버피팅으로 이어질 수 있다.

2) 기울기 소실이 일어나기 쉬워지고, 그럼 학습이 불안정해진다.

3) 파라미터가 많은 모델은 당연히 학습 시간이 길어진다.

[3]Attention is all you need로부터 영감을 받아, 아래와 같이 처리하여 이 문제들을 해결한다!

$$ g(x) = x + \text{Dropout}(g(\text{LayerNorm}(x))) $$

$g(x)$는 셀프어텐션 레이어 또는 피드포워드 신경망을 나타낸다. 즉, 셀프어텐션이나 피드포워드 신경망을 지날 때마다, [layer normalization → 셀프어텐션 or 피드포워드 신경망 → 드랍아웃 → 잔차연결] 까지가 한 세트가 되는 것이다.

D. Prediction Layer

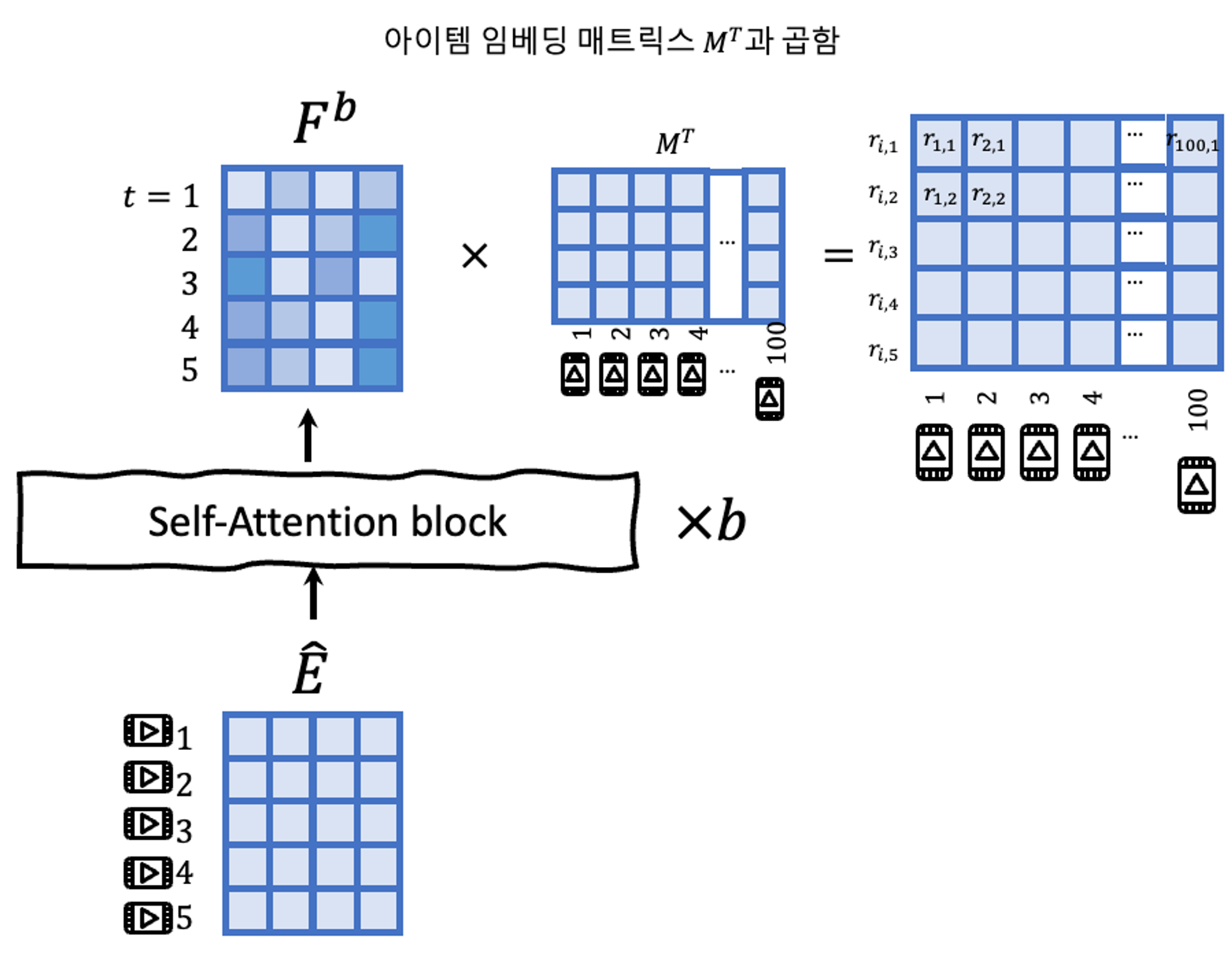
$b$개의 셀프어텐션 블록을 지나고 나면 $\mathbf{F}^{(b)}$를 얻을 수 있다! 우린 $\mathbf{F}^{(b)}$의 마지막 아이템 위치의 벡터인 $\mathbf{F}^{(b)}_t$를 이용해서 다음 아이템을 예측할건데, $\mathbf{F}^{(b)}_t$는 앞의 아이템들의 정보를 모두 갖고있기 때문이다.

Shared Item Embedding

모델 사이즈를 줄이고 오버피팅을 막기 위해, 아이템 임베딩 $\mathbf{M}$만 사용한다! 그래서 prediction layer는 아래와 같이 된다. A.Embedding Layer에서 $\mathbf{M} \in \mathbb{R}^{|\mathcal{I}| \times d}$를 아이템 임베딩 벡터라고 했었다.

$$ r_{i,t}=\mathbf{F}_t^{(b)}\mathbf{M}_i^T $$

$r_{i,t}$는 아이템 $i$가 다음 아이템으로 적절한지를 나타내는 수, relevance이다.

이렇게 인풋레이어와 예측레이어에서 같은 임베딩 벡터를 쓸 때 발생할 수 있는 잠재적인 문제는 무엇일까? 아이템 벡터간의 내적이 비대칭적 순서를 나타내지 못한다는 것이다. 예를 들어 $i$는 $j$ 뒤에 자주 나왔는데, 반대는 아닌 경우이다. 그러므로 FPMC같은 기존 모델은 동질적인(heterogeneous) 아이템 임베딩이 되는 경향이 있다. 그러나, SASRec은 비선형적 변형을 학습하기 때문에 이런 이슈가 없다. 예를 들면 피드포워드 신경망은 비대칭성을 쉽게 달성할 수 있다:

$$ \text{FFN}(\mathbf{M}_i)\mathbf{M}_j^T \ne \text{FFN}(\mathbf{M}_j)\mathbf{M}_i^T $$

경험적으로 아이템 임베딩을 공유하는 것은 SASRec의 성능을 매우 향상시켰다!

E. Network Training

유저 $u$의 시퀀스를 $\mathcal{S}^u$라고 했었다. $\mathcal{S}^u = (\mathcal{S}_1^u, \mathcal{S}_2^u, ..., \mathcal{S}_{|\mathcal{S}^u|}^u)$. 모델 인풋 학습데이터는 마지막 하나를 뺀 $(\mathcal{S}_1^u, \mathcal{S}_2^u, ..., \mathcal{S}_{|\mathcal{S}^u-1|}^u)$이다. 그리고 이 시퀀스에서 최근 $n$개만 사용한다. 이렇게 변환한 시퀀스를 $s=\{s_1, s_2, ..., s_n \}$라고 표기하자. $n$개가 안되면 패딩을 하기 때문에 앞의 $s_1, s_2$등등은 패딩인덱스일 수도 있다. $1\le t \lt n$에 대하여, 예측되는 아웃풋을 $o_t$라고 표기해보자.

$$ o_t = \begin{cases} \langle \text{pad} \rangle & \text{if } s_t \text{ is padding item} \\ s_{t+1} & 1 \le t < n \\ \mathcal{S}^u_{|\mathcal{S}^u|} & t = n \end{cases} $$

loss로는 binary cross entropy를 사용한다!

$$ -\sum_{\mathcal{S}^u \in \mathcal{S}} \sum_{t \in [1, 2, ..., n]} \left[ \log{(\sigma(r_{o_t, t})) + \sum_{j \notin \mathcal{S}^u}} \log{(1-\sigma(r_{j,t}))} \right] $$

$o_t=\langle \text{pad} \rangle$일 때는 해당 텀을 무시한다! $j$는 네거티브 아이템을 의미한다. 시퀀스 속의 아이템 하나 당 네거티브 아이템 하나를 선정하는데, 각 에폭마다 랜덤하게 뽑는다.

옵티마이저는 Adam을 사용.

F. Complexity Analysis

공간복잡도 : 학습되는 파라미터는 임베딩, 셀프어텐션, 피드포워드 네트워크, layer normalization이다. 이 수를 합하면 $O(|\mathcal{I}|d + nd + d^2)$이며, FPMC같은 여타 다른 모델과 비교해도 적당하다!

시간복잡도 : 본 모델의 시간복잡도는 $O(n^2 d + n d^2)$이며 이는 주로 셀프어텐션과 피드포워드 때문이다. 이 중에 메인 텀은 $O(n^2d)$인데, 셀프어텐션 부분이다. 그런데 셀프어텐션은 병렬처리가 가능하다! 반면 GRU4Rec같은 RNN 기반의 모델은 시퀀스 길이에 의존적이기 때문에, SASRec이 RNN, CNN기반 모델보다 10배는 빠르다!

G. Discussion

Reduction to Existing Models

MC-based Recommendation

RNN-based Recommendation

IV. EXPERIMENTS

Research Questions

RQ1. SASRec은 CNN/RNN 기반 모델을 포함해 최신 모델을 능가하는가?

RQ2. SASRec 구조 속의 다양한 컴포넌트들의 영향력은 얼마나 되는가?

RQ3. SASRec의 학습효율 및 ($n$에 대한) 확장성은 어떨까?

RQ4. 어텐션 가중치는 아이템의 어트리뷰트 또는 위치와 연관된 정보를 반영할까?

A. Datasets

• Amazon
• Steam
• MovieLens

B. Comparison Methods

• First Group : 유저 피드백만 고려할 뿐, 시퀀스 순서는 고려하지 않음
  • PopRec : 인기도 정렬
  • BPR(Bayesian Personalized Ranking)
• Second Group : 마지막 아이템만 고려하는 1차 마르코프 체인에 기반한 시퀀셜 추천
  • FMC (Factorized Markov Chains)
  • FPMC (Factorized Personalized Markov Chains)
  • TransRec (Translation-based Recommendation)
• Last group : 모든 아이템을 고려하는 시퀀셜 추천
  • GRU4Rec
  • GRU4Rec$^+$ : GRU4Rec과 손실함수, 샘플링이 다름
  • Caser (Convolutional Sequence Embeddings)

C. implementation Details

• 셀프어텐션 블록 2개 사용($b=2$)
• 학습가능한 포지셔널 임베딩 사용
• 임베딩 레이어와 예측 레이어의 아이템 임베딩은 공유
• 옵티마이저는 Adam 사용.
• learning rate는 0.001
• 배치사이즈는 128
• 드랍아웃 비율은 데이터셋의 희소성에 따라 0.2 또는 0.5를 사용한다.
• 최대 길이 $n$은 ML-1M에는 200을, 다른 세 데이터셋에 대해서는 50을 사용한다. 이는 유저 액션 길이 평균값으로 맞춘 것이다!

D. Evaluation Metrics

• Hit Rate@10 : 예측아이템 상위 10개 아이템 중 정답아이템이 존재하면 1, 아니면 0. 전체 데이터셋에 대해서 비율을 계산!
• NDCG@10 : 예측아이템 상위 10개 아이템 중 정답아이템의 순위가 높을수록 높게 계산됨

E. Recommendation Performance

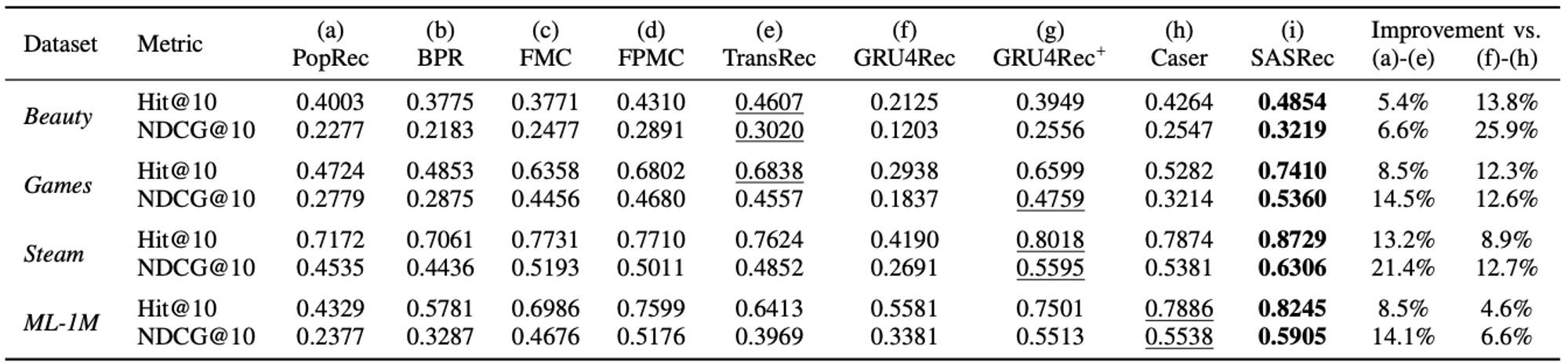
RQ1 해결. 성능 향상이 최소 5프로에서 최대21퍼까지……ㄷㄷ

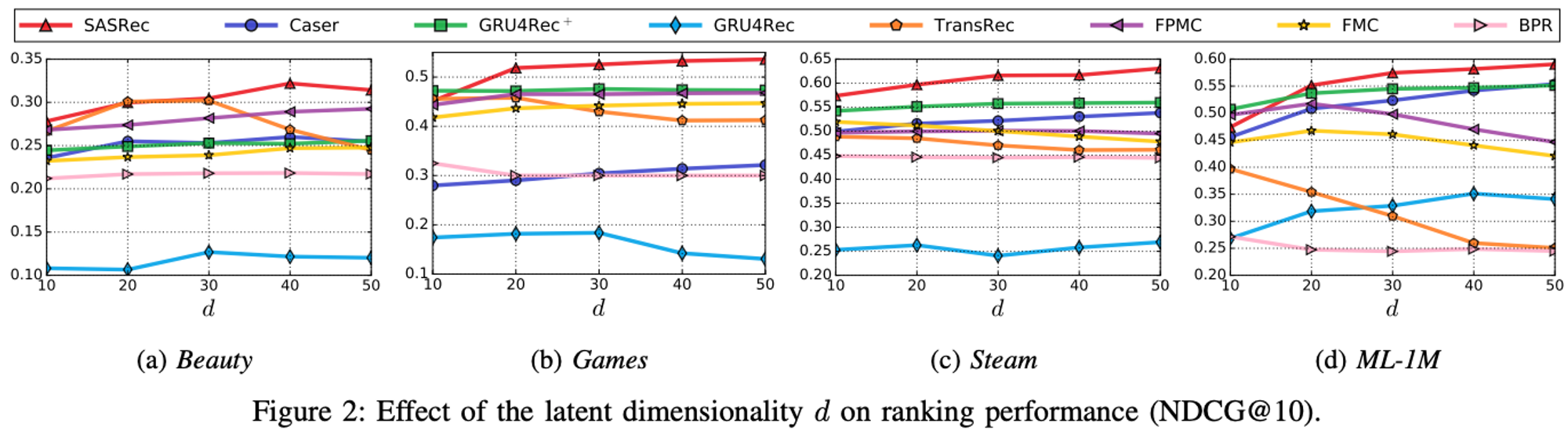
임베딩 차원을 다양하게 바꿔가며 실험해봤을때, SASRec은 차원을 높일수록 성능이 좋아졌으며, 40이상이 최적값으로 보임.

---